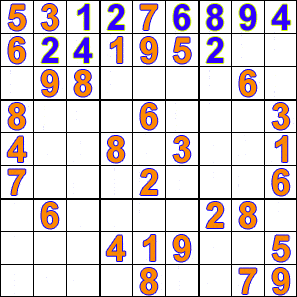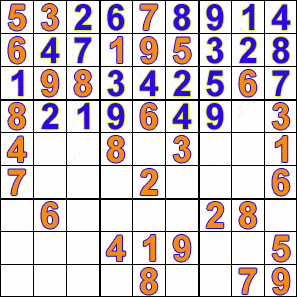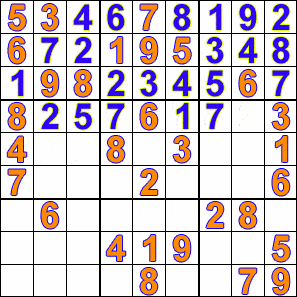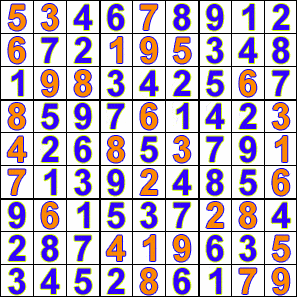
Sudoku is a fun logic-based puzzle in which the objective is to fill a 9×9 grid with digits from 1-9 in such a way that no digit is repeated in the same row, column or 3×3 box.
In this post, I will show you how we can solve sudoku using a backtracking algorithm.
What is Backtracking?
Backtracking is a general algorithm for finding all (or some) solutions to some computational problems, notably constraint satisfaction problems,
Donald E. Knuth (1968). The Art of Computer Programming. Addison-Wesley.
that incrementally builds candidates to the solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution.
A backtracking approach is a step better than a naive brute force search algorithm. In a brute force search, we would have to generate all possible variations of a sudoku board and then choose a valid solution. With backtracking, we only keep valid boards so at any given time the sudoku grid is always correct.
The Algorithm
- Find the first empty square
- If there are no empty square that means that the board is full and since we only keep valid solutions, the sudoku is solved and we are done! Return True.
- If an empty square exists – try filling it with a number from [1-9]
- Check to see if the board is valid (the number is not repeated in the same row, column or 3×3 box)
- If we have a valid board from step 4, Goto Step 1
- If we don’t have a valid board from step 4, un-assign the number from the square and backtrack to step 3, trying with a different number
- If you have reached this step- there is no solution. Return False.
The Code
Let’s begin coding. First, we need a way to represent the sudoku board, we can do this using a 2D array, we will also need some helper functions to check if a board is valid and another function to print the solved board for us.
| #!/usr/bin/env python | |
| def print_board(board): | |
| for row in board: | |
| for col in row: | |
| print(col, end=" ") | |
| print("\n") | |
| def find_empty_square(board): | |
| """ | |
| Return a tuple containing the row and column of the first empty square | |
| False if no squares are empty | |
| """ | |
| for i, row in enumerate(board): | |
| for j, square in enumerate(row): | |
| if square == 0: | |
| return (i, j) | |
| return False | |
| def num_in_row(board, row, num): | |
| """True if num is already in the row, False otherwise""" | |
| return num in board[row] | |
| def num_in_col(board, col, num): | |
| """True if num is already in the column, False otherwise""" | |
| return num in [row[col] for row in board] | |
| def num_in_box(board, row, col, num): | |
| """ | |
| row and col should be the top-left coordinates of the box | |
| True if num is already in the 3x3 box, False otherwise | |
| """ | |
| return num in [board[row+i][col+j] for i in range(3) for j in range(3)] | |
| def safe_position(board, row, col, num): | |
| """ | |
| A safe position is one in which a number can be placed without being | |
| repeated in the same row, column or 3x3 box | |
| True if position is safe, False otherwise | |
| """ | |
| return not num_in_row(board, row, num) \ | |
| and not num_in_col(board, col, num) \ | |
| and not num_in_box(board, row - row %3, col - col %3, num) | |
| def solve_sudoku(board): | |
| """Returns True if a solution exists False otherwise""" | |
| next_empty_square = find_empty_square(board) | |
| if not next_empty_square: # The board is full/solved | |
| return True | |
| row, col = next_empty_square | |
| for num in range(1, 10): | |
| if safe_position(board, row, col, num): | |
| board[row][col] = num | |
| if solve_sudoku(board): | |
| return True | |
| board[row][col] = 0 # invalid position, unnasign the number | |
| return False # backtrack and try another number | |
| def main(): | |
| grid = [[0,2,6,0,0,0,8,1,0], | |
| [3,0,0,7,0,8,0,0,6], | |
| [4,0,0,0,5,0,0,0,7], | |
| [0,5,0,1,0,7,0,9,0], | |
| [0,0,3,9,0,5,1,0,0], | |
| [0,4,0,3,0,2,0,5,0], | |
| [1,0,0,0,3,0,0,0,2], | |
| [5,0,0,2,0,4,0,0,9], | |
| [0,3,8,0,0,0,4,6,0]] | |
| if solve_sudoku(grid): | |
| print_board(grid) | |
| else: | |
| print("No solution exists!") | |
| if __name__ == '__main__': | |
| main() |
This is just one way of solving sudoku, for a more efficient algorithm be sure to check out this essay by Peter Norvig. It uses constraint propagation and search, to solve the worlds hardest sudoku puzzles in a tenth of a second!